Want to make sure you win the coin toss just a little more often than you should? I certainly do, so I made some unfair coins. We’ll use the beta distribution to see just how unfair they are. While this is just a toy example problem for using the beta distribution, machine learning algorithms rely on this distribution for learning just about everything. Math is an amazing thing that way.
Making the coins
We’ll make our unfair coins by bending them. Our hypothesis is that the concave side will have less area to land on, and so the coin should land on it less often. Let’s get started.
It’s easy to bend the coins with your teeth:
WAIT! That really hurts! Using pliers or wrenches works much better:
I made seven coins this way, each with a different bending angle.
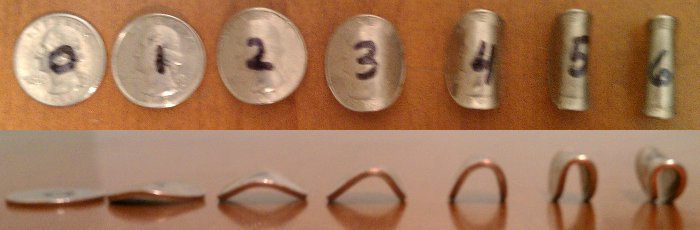
I did 100 flips for each coin, making sure each flip went at least a foot in the air and spun real well. “Umm… only 100 flips?” you ask, “That can’t be enough!” Just you wait until the section on the math.
Here’s the raw results:
| Coin | Total Flips | Heads | Tails |
| 0 | 100 | 53 | 47 |
| 1 | 100 | 55 | 45 |
| 2 | 100 | 49 | 51 |
| 3 | 100 | 41 | 59 |
| 4 | 100 | 39 | 61 |
| 5 | 100 | 27 | 73 |
| 6 | 100 | 0 | 100 |
Now for the math
Coin flipping is a Bernoulli process. This just means that all trials (flips) can have only two outcomes (heads or tails), and each trial is independent of every other trial. What we’re interested in calculating is the expected value of a coin flip for each of our coins. That is, what is the probability it will come up heads? The obvious way to calculate this probability is simply to divide the number of heads by the total number of trials. Unfortunately, this doesn’t give us a good idea about how accurate our estimate is.
Enter the beta distribution. This is a distribution over the bias of a Bernoulli process. Intuitively, this means that CDF(x) equals the probability that the expectation of a coin flip is x. In other words, we’re finding the probability that a probability is what we think it should be. That’s a convoluted definition! Some examples should make it clearer.
The beta distribution takes two parameters and . is the number of heads we have flipped plus one, and is the number of tails plus one. We’ll talk about why that plus one is there in a bit, but first let’s see what the distribution actually looks like with some example parameters.
In both the above cases, the distribution is centered around 0.5 because and are equal—we’ve gotten the same number of heads as we have tails. As these parameters increase, the distribution gets tighter and tighter. This should makes sense. The more flips we do, the more confident we can be that the data we’ve collected actually match the characteristics of the coin.
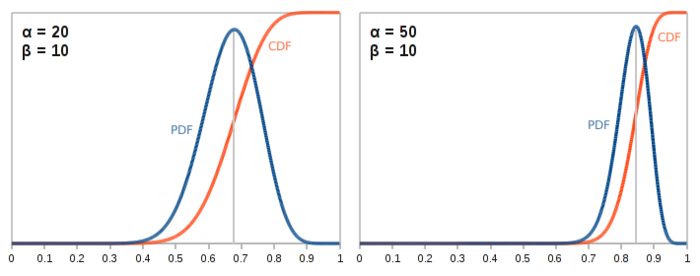
When the parameters are not equal to each other—for example, we’ve seen twice as many heads as we have tails—then the distribution is skewed to the left or right accordingly. The peak of the PDF occurs at:
That’s exactly what we said the expectation of the next coin flip should be above. Awesome!
So what happens when and are one?
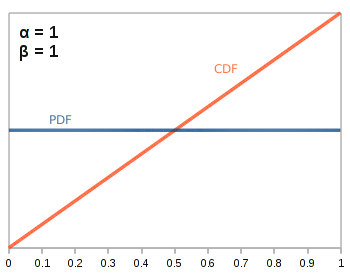
We get the flat distribution. Basically, we haven’t flipped the coin at all yet, so we have no data about how our coin is biased, so all biases are equally likely. This is why we must add one to the number of heads and tails we have flipped to get the appropriate and .
If and are less than one, we get something like this:
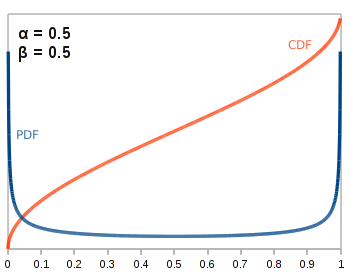
Essentially, this means that we know our coin is very biased in one way or the other, but we don’t know which way yet! As you can imagine, such perverse parameterizations are rarely used in practice.
Hopefully, this has given you an intuitive sense for what the beta distribution looks like. But for the pedantic, here’s how the beta distribution’s pdf is formally defined:
Where is the gamma function—you can think of it as being a generalization of factorials to the real numbers. That is, . Excel, many calculators, and any scientific programming package will be able to calculate that for you easily. Most of these applications will even have the beta function already built in.
Applying the beta distribution to our coins
We’re finally ready to see just how biased our coins actually are!
|
Coin 0
Heads: 53 Tails: 47 |
 |
|
Coin 1 Heads: 55 Tails: 45 |
 |
|
Coin 2
Heads: 49 Tails: 51 |
 |
|
Coin 3 Heads: 41 Tails: 59 |
 |
|
Coin 4 Heads: 39 Tails: 61 |
 |
|
Coin 5 Heads: 27 Tails: 73 |
 |
|
Coin 6 Heads: 0 Tails: 100 |
 |
Amazingly, it takes some pretty big bends to make a biased coin. It is not until coin 3, which has an almost 90 degree bend that we can say with any confidence that the coin is biased at all. People might notice if you tried to flip that coin to settle a bet!
-
This is great. I really enjoyed this post.
Here is my crack at the para describing the meaning of the beta function (“Enter the beta distribution. …. “):
Enter the beta distribution. Given our observation of H heads and T tails, this distribution allows us to plot how likely a given fraction of heads (or tails) is going to be.
If the beta distribution is narrow, which happens when we have many observations, we can be pretty sure of where the “real” fraction of heads lies.
If the beta distribution is wide (when we have few observations), our margin of uncertainty gets larger.
(As a side note, I think the CDF might detract from the expostion).
Any how, once again, I really enjoyed your experiment!
Best wishes.
-
Yeah, that was by far the hardest paragraph to write in the whole thing. It probably only makes sense if you already know what I’m trying to say
-
-
If you’re into more analytic solutions, check out the wikipedia article where they perform all the calculations and proofs.
http://en.wikipedia.org/wiki/Checking_whether_a_coin_is_fair#Posterior_probability_density_function
-
Would have been nice to mention that the beta function there is not magic — the terms involving x are proportional to the probability of flipping that many heads/tails for a particular underlying rate x, and the gamma function terms are a normalization such that, when integrated over all x, you get a net probability of 1.
-
Your expression for the pdf is slightly wrong. The denominator should be
\Gamma(\alpha) \times \Gamma(\beta),
not
\Gamma(\alpha) \plus \Gamma(\beta).
-
Fixed. Thanks.
-
-
You say that people concerned about whether 100 flips is enough should “wait until the section on the math”. Then you find that for the mildly bent coins you don’t have enough data to determine if they are biased. I would guess that with more trials you could find a bias in coins 1 and 2.
-
That’s probably true, but the number of trials required would be WAY more than I was willing to do. For example, if you set alpha = 2000 and beta = 2100, you still couldn’t say with 95% confidence that the coin was biased. That’s over four thousand flips.
So you’re right. If the coin is only slightly biased, then 100 flips is no where near enough. But with a large enough bias, it becomes sufficient.
-
-
> Our hypothesis is that the concave side will have less area to land on, and so the coin should land on it less often.
The result is correct, but (for a modestly bent coin) the reasoning is not. The reason a bent coin prefers to land on its convex side is because when it strikes the surface on its edge, it tends to fall toward the convex side for simple reasons of balance and mass distribution (the center of mass is biased toward the convex side compared to the mean of the circumference).
Also, while in flight, a bent coin tends to align itself in the air with its convex side down just as a falling leaf does, and for the same reason — simple aerodynamics. If an experimenter flipped a coin from a great height, most of the coins would eventually stop flipping and stabilize convex side down.
-
The result is correct, but the reasoning is not….
I believe your explanation and the hypothesis are actually equivalent statements, at least in the mathematical sense if not the physical sense.
Also, while in flight, a bent coin tends to align itself in the air with its convex side down
Wouldn’t it align edge side down? Unlike the leaf, it’s rather heavy.
-
-
I am curious about your flipping method. did you always start on heads/tails, alternate between tosses or flip from the resulting orientation of the previous toss? it would be interesting to see if different methods produced a bias
-
That’s a great point. I made no special effort to control the starting position of the flips. Some of the latter coins were very awkward to flip with the concave side down, so I probably flipped concave side up most of the time for these.
I doubt that starting on heads/tails would make a difference, but I do think the orientation of the bend axis relative to your thumb might. For example, I would guess that flipping so that the coin spins about the bend axis would enhance the coin’s bias relative to spinning perpendicular to the spin axis.
-
-
How were the coins landed? Bounced? Cushioned? I think how it settles is where the determination mostly occurs, rather than in flight. A coin bent like a cardioid has to settle always the same way (approximately like coin 6). Your coins are all degrees of cardioid.
Jaymz
-
They landed on a wooden table covered by a table cloth. They bounced a little, but not too much.
-
-
Hi Mike,
Talking about unfair coins.
Supose we know a coin is unfair but we don’t know how biased it is.
We perform the bernoulli experiment flipping the biased coin 100 times.
We get +4 standard deviations for head hits.
But, with this small sample we cannot certify that heads will hit +4 sd again.
We only know it is biased but we do not know how much because fluctuations can fool you easily when you are not an expert.
What we also know is that the mean is not 50/100 but a higher number more than 50 of 100.
How can we know the real deviation from the real mean?
The number of 100-toss experiments will depend on the strentgh of the bias.
Is there a way to guess or calculate the bounderies of this coin when we already know it is unfair and we have performed several tests?
How many?
Best regards.
Thanks in advance-
That’s exactly what the beta distribution is for. We can’t say with 100% certainty exactly what the coin’s bias is, but we can use the beta distribution to say it has e.g. a 56% chance of having a bias greater than 52%. You would have to do many more trials after getting only 54/100 heads. That’s not enough to indicate a reasonable chance that there even is a bias.
-
-
So, having more trials, we could be closer to a conclusion.
In my question we are 100% sure the coin is biased.
What we want to know is in what bounderis the bias is(+1% to +3% or +10 to 15%)
in what i work I need to identify the degree of bias to decide what to do.
can it be done?-
>In my question we are 100% sure the coin is biased.
I highly doubt that you are that sure the coin is biased. But if you insist, what you would do is to “chop off” the part of the beta distribution that goes below 50% and then renormalize.
-
Then, the degree are from 51% to whatever(80%).
My intencion is to cut out the 51 to 54% and take the over 55% chance. I mean +10% the normal distribution.
Is there a way to know the strentgh of the bias?-
I’m sorry I don’t understand what you’re trying to do, and probably won’t be able to help you.
-
-
-
-
Hello, the following side might be interesting for those
who liked Mike’s experiment.http://www.stat.columbia.edu/~gelman/research/published/diceRev2.pdf
“You can load a die, but you can not bias a coin” is,
what the authors claim.Their statement is pretty in line with Mike’s observation
“Amazingly, it takes some pretty big bends to make a biased coin.”By the way, you can “load” wooden dice very easily by watering them
for 24 hours.Ingo.
21 comments
Comments feed for this article
Trackback link: http://izbicki.me/blog/how-to-create-an-unfair-coin-and-prove-it-with-math/trackback