Fast Nearest Neighbor Queries in Haskell
Two weeks ago at ICML, I presented a method for making nearest neighbor queries faster. The paper is called Faster Cover Trees and discusses some algorithmic improvements to the cover tree data structure. You can find the code in the HLearn library on github.
The implementation was written entirely in Haskell, and it is the fastest existing method for nearest neighbor queries in arbitrary metric spaces. (If you want a non-Haskell interface, the repo comes with a standalone program called hlearn-allknn for finding nearest neighbors.) In this blog post, I want to discuss four lessons learned about using Haskell to write high performance numeric code. But before we get to those details, let’s see some benchmarks.
The benchmarks
The benchmark task is to find the nearest neighbor of every point in the given dataset. We’ll use the four largest datasets in the mlpack benchmark suite and the Euclidean distance. (HLearn supports other distance metrics, but most of the compared libraries do not.) You can find more details about the compared libraries and instructions for reproducing the benchmarks in the repo’s bench/allknn folder.
the runtime of finding every nearest neighbor


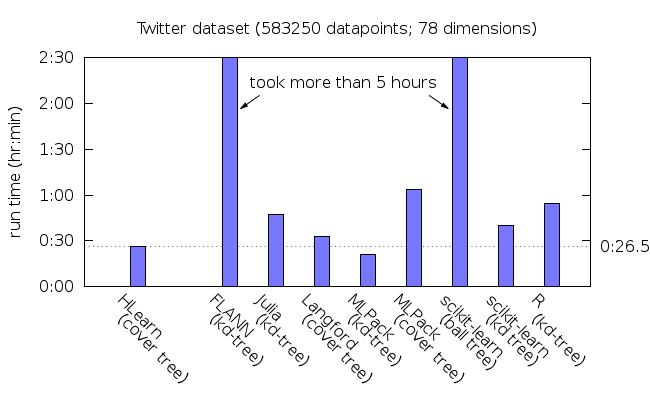

Notice that HLearn’s cover trees perform the fastest on each dataset except for YearPredict. But HLearn can use all the cores on your computer to parallelize the task. Here’s how performance scales with the number of CPUs on an AWS EC2 c3.8xlarge instance with 16 true cores:

With parallelism, HLearn is now also the fastest on the YearPredict dataset by a wide margin. (FLANN is the only other library supporting parallelism, but in my tests with this dataset parallelism actually slowed it down for some reason.)
You can find a lot more cover tree specific benchmarks in the Faster Cover Trees paper.
The lessons learned
The Haskell Wiki’s guide to performance explains the basics of writing fast code. But unfortunately, there are many details that the wiki doesn’t cover. So I’ve selected four lessons from this project that I think summarize the state-of-the-art in high performance Haskell coding.
Lesson 1: Polymorphic code in GHC is slower than it needs to be.
Haskell makes generic programming using polymorphism simple. My implementation of the cover tree takes full advantage of this. The CoverTree_ type implements the data structure that speeds up nearest neighbor queries. It is defined in the module HLearn.Data.SpaceTree.CoverTree as:
data CoverTree_
( childC :: * -> * ) -- the container type to store children in
( leafC :: * -> * ) -- the container type to store leaves in
( dp :: * ) -- the type of the data points
= Node
{ nodedp :: !dp
, level :: {-#UNPACK#-}!Int
, nodeWeight :: !(Scalar dp)
, numdp :: !(Scalar dp)
, maxDescendentDistance :: !(Scalar dp)
, children :: !(childC (CoverTree_ childC leafC dp))
, leaves :: !(leafC dp)
}Notice that every field except for level is polymorphic. A roughly equivalent C++ struct (using higher kinded templates) would look like:
template < template <typename> typename childC
, template <typename> typename leafC
, typename dp
>
struct CoverTree_
{
dp *nodedp;
int level;
dp::Scalar *nodeWeight;
dp::Scalar *numdp;
dp::Scalar *maxDescendentDistance;
childC<CoverTree_<childC,leafC,dp>> *children;
leafC<dp> *leaves;
}Notice all of those nasty pointers in the C++ code above. These pointers destroy cache performance for two reasons. First, the pointers take up a significant amount of memory. This memory fills up the cache, blocking the data we actually care about from entering cache. Second, the memory the pointers reference can be in arbitrary locations. This causes the CPU prefetcher to load the wrong data into cache.
The solution to make the C++ code faster is obvious: remove the pointers. In Haskell terminology, we call this unpacking the fields of the Node constructor. Unfortunately, due to a bug in GHC (see issues #3990 and #7647 and a reddit discussion), these polymorphic fields cannot currently be unpacked. In principle, GHC’s polymorphism can be made a zero-cost abstraction similar to templates in C++; but we’re not yet there in practice.
As a temporary work around, HLearn provides a variant of the cover tree specialized to work on unboxed vectors. It is defined in the module HLearn.Data.SpaceTree.CoverTree_Specialized as:
data CoverTree_
( childC :: * -> * ) -- must be set to: BArray
( leafC :: * -> * ) -- must be set to: UArray
( dp :: * ) -- must be set to: Labaled' (UVector "dyn" Float) Int
= Node
{ nodedp :: {-#UNPACK#-}!(Labeled' (UVector "dyn" Float) Int)
, nodeWeight :: {-#UNPACK#-}!Float
, level :: {-#UNPACK#-}!Int
, numdp :: {-#UNPACK#-}!Float
, maxDescendentDistance :: {-#UNPACK#-}!Float
, children :: {-#UNPACK#-}!(BArray (CoverTree_ exprat childC leafC dp))
, leaves :: {-#UNPACK#-}!(UArray dp)
}Since the Node constructor no longer has polymorphic fields, all of its fields can be unpacked. The hlearn-allknn program imports this specialized cover tree type, giving a 10-30% speedup depending on the dataset. It’s a shame that I have to maintain two separate versions of the same code to get this speedup.
Lesson 2: High performance Haskell code must be written for specific versions of GHC.
Because Haskell code is so high level, it requires aggressive compiler optimizations to perform well. Normally, GHC combined with LLVM does an amazing job with these optimizations. But in complex code, sometimes these optimizations don’t get applied when you expect them. Even worse, different versions of GHC apply these optimizations differently. And worst of all, debugging problems related to GHC’s optimizer is hard.
I discovered this a few months ago when GHC 7.10 was released. I decided to upgrade HLearn’s code base to take advantage of the new compiler’s features. This upgrade caused a number of performance regressions which took me about a week to fix. The most insidious example happened in the findNeighbor function located within the HLearn.Data.SpaceTree.Algorithms module. The inner loop of this function looks like:
go (Labeled' t dist) (Neighbor n distn) = if dist*ε > maxdist
then Neighbor n distn
else inline foldr' go leafres
$ sortBy (\(Labeled' _ d1) (Labeled' _ d2) -> compare d2 d1)
$ map (\t' -> Labeled' t' (distanceUB q (stNode t') (distnleaf+stMaxDescendentDistance t)))
$ toList
$ stChildren t
where
leafres@(Neighbor _ distnleaf) = inline foldr'
(\dp n@(Neighbor _ distn') -> cata dp (distanceUB q dp distn') n)
(cata (stNode t) dist (Neighbor n distn))
(stLeaves t)
maxdist = distn+stMaxDescendentDistance tFor our purposes right now, the important thing to note is that go contains two calls to foldr': one folds over the CoverTree_’s childC, and one over the leafC. In GHC 7.8, this wasn’t a problem. The compiler correctly specialized both functions to the appropriate container type, resulting in fast code.
But for some reason, GHC 7.10 did not want to specialize these functions. It decided to pass around huge class dictionaries for each function call, which is a well known cause of slow Haskell code. In my case, it resulted in more than a 20 times slowdown! Finding the cause of this slowdown was a painful exercise in reading GHC’s intermediate language core. The typical tutorials on debugging core use trivial examples of only a dozen or so lines of core code. But in my case, the core of the hlearn-allknn program was several hundred thousand lines long. Deciphering this core to find the slowdown’s cause was one of my more painful Haskell experiences. A tool that analyzed core to find function calls that contained excessive dictionary passing would make writing high performance Haskell code much easier.
Once I found the cause of the slowdown, fixing it was trivial. All I had to do was call the inline function on both calls to foldr. In my experience, this is a common theme in writing high performance Haskell code: Finding the cause of problems is hard, but fixing them is easy.
Lesson 3: Immutability and laziness can make numeric code faster.
The standard advice in writing numeric Haskell code is to avoid laziness. This is usually true, but I want to provide an interesting counter example.
This lesson relates to the same go function above, and in particular the call to sortBy. sortBy is a standard Haskell function that uses a lazy merge sort. Lazy merge sort is a slow algorithm—typically more than 10 times slower than in-place quicksort. Profiling hlearn-allknn shows that the most expensive part of nearest neighbor search is calculating distances (taking about 80% of the run time), and the second most expensive part is the call to sortBy (taking about 10% of the run time). But I nevertheless claim that this lazy merge sort is actually making HLearn’s nearest neighbor queries much faster due to its immutability and its laziness.
We’ll start with immutability since it is pretty straightforward. Immutability makes parallelism easier and faster because there’s no need for separate threads to place locks on any of the containers.
Laziness is a bit trickier. If the explanation below doesn’t make sense, reading Section 2 of the paper where I discuss how a cover tree works might help. Let’s say we’re trying to find the nearest neighbor to a data point we’ve named q. We can first sort the children according to their distance from q, then look for the nearest neighbors in the sorted children. The key to the cover tree’s performance is that we don’t have to look in all of the subtrees. If we can prove that a subtree will never contain a point closer to q than a point we’ve already found, then we “prune” that subtree. Because of pruning, we will usually not descend into every child. So sorting the entire container of children is a waste of time—we should only sort the ones we actually visit. A lazy sort gives us this property for free! And that’s why lazy merge sort is faster than an in-place quick sort for this application.
Lesson 4: Haskell’s standard libraries were not designed for fast numeric computing.
While developing this cover tree implementation, I encountered many limitations in Haskell’s standard libraries. To work around these limitations, I created an alternative standard library called SubHask. I have a lot to say about these limitations, but here I’ll restrict myself to the most important point for nearest neighbor queries: SubHask lets you safely create unboxed arrays of unboxed vectors, but the standard library does not. (Unboxed containers, like the UNPACK pragma mentioned above, let us avoid the overhead of indirections caused by the Haskell runtime. The Haskell wiki has a good explanation.) In my experiments, this simple optimization let me reduce cache misses by around 30%, causing the program to run about twice as fast!
The distinction between an array and a vector is important in SubHask—arrays are generic containers, and vectors are elements of a vector space. This distinction is what lets SubHask safely unbox vectors. Let me explain:
In SubHask, unboxed arrays are represented using the UArray :: * -> * type in SubHask.Algebra.Array. For example, UArray Int is the type of an unboxed array of ints. Arrays can have arbitrary length, and this makes it impossible to unbox an unboxed array. Vectors, on the other hand, must have a fixed dimension. Unboxed vectors in SubHask are represented using the UVector :: k -> * -> * type in SubHask.Algebra.Vector. The first type parameter k is a phantom type that specifies the dimension of the vector. So a vector of floats with 20 dimensions could be represented using the type UVector 20 Float. But often the size of a vector is not known at compile time. In this case, SubHask lets you use a string to identify the dimension of a vector. In hlearn-allknn, the data points are represented using the type UVector "dyn" Float. The compiler then statically guarantees that every variable of type UVector "dyn" Float will have the same dimension. This trick is what lets us create the type UArray (UVector "dyn" Float).
The hlearn-allknn program exploits this unboxing by setting the leafC parameter of CoverTree_ to UArray. Then, we call the function packCT which rearranges the nodes in leafC to use the cache oblivious van Embde Boas tree layout. Unboxing by itself gives a modest 5% performance gain from the reduced overhead in the Haskell run time system; but unpacking combined with this data rearrangement actually cuts runtime in half!
Unfortunately, due to some current limitations in GHC, I’m still leaving some performance on the table. The childC parameter to CoverTree_ cannot be UArray because CoverTree_s can have a variable size depending on their number of children. Therefore, childC is typically set to the boxed array type BArray. The GHC limitation is that the run time system gives us no way to control where the elements of a BArray exist in memory. Therefore, we do not get the benefits of the CPU prefetcher. I’ve proposed a solution that involves adding new primops to the GHC compiler (see feature request #10652). Since there are typically more elements within the childC than the leafC on any given cover tree, I estimate that the speedup due to better cache usage of BArrays would be even larger than the speedup reported above.
Conclusion
My experience is that Haskell can be amazingly fast, but it takes a lot of work to get this speed. I’d guess that it took about 10 times as much work to create my Haskell-based cover tree than it would have taken to create a similar C-based implementation. (I’m roughly as proficient in each language.) Furthermore, because of the current limitations in GHC I pointed out above, the C version would be just a bit faster.
So then why did I use Haskell? To make cover trees 10 times easier for programmers to use.
Cover trees can make almost all machine learning algorithms faster. For example, they’ve sped up SVMs, clustering, dimensionality reduction, and reinforcement learning. But most libraries do not take advantage of this optimization because it is relatively time consuming for a programmer to do by hand. Fortunately, the fundamental techniques are simple enough that they can be implemented as a compiler optimization pass, and Haskell has great support for libraries that implement their own optimizations. So Real Soon Now (TM) I hope to show you all how cover trees can speed up your Haskell-based machine learning without any programmer involvement at all.